In this blog post, I hope to give a brief introduction to isogeny-based cryptography, and introduce the idea behind the SIDH scheme.

Background

An elliptic curve \(E(K)\) over a field \(K\), or just \(E = E(\overline{K})\), is (roughly) the set of solutions \((x, y) \in K^2\) of the equation \(y^2 = x^3 + ax + b\). It has an abelian group structure, i.e. an identity \(O\) and an operation \(+ : E(K) \to E(K) \to E(K)\) satisfying the abelian group axioms, e.g. \(P + Q = Q + P\) and \(P + (Q + R) = (P + Q) + R\), etc. Since \(K\) is finite, our curve \(E(K)\) is also finite. In classical cryptography (pre-quantum), we perform operations on this group structure. For example, we can think about the discrete logarithm problem:

With our current computers, the problem is hard. In fact, we don’t know how to solve this better than the generic Pohlig-Hellman algorithm. However, the story changes when we introduce quantum computers, as Shor’s Algorithm provides a polynomial-time algorithm to solve the discrete logarithm problem. Hence, we turn to the so-called post-quantum cryptography, and isogeny-based cryptography is one of the promising candidates.

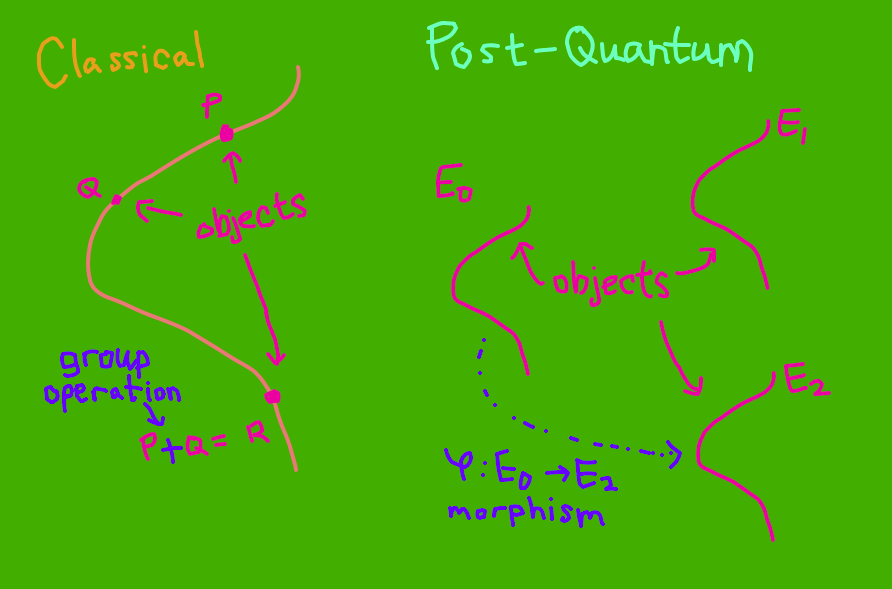
The philosophy of isogeny-based cryptography is simple: instead of taking \(E\) as our “cryptography group”, we instead take the set of all elliptic curves. That is, instead of having points \(P, Q, R, \cdots \in E\), we now have \(E_0, E_1, E_2, \cdots \in \mathcal{Ell}_K\). But this is not useful yet. How do we create cryptography out of these curves? Well, we work with morphisms between curves! In the diagram below, things drawn in magenta are the objects, while things drawn in blue are how we manipulate them.

What are Isogenies?

There are many definitions and/or properties of isogenies separable . They are morphisms, group homomorphisms with finite kernel, rational maps, etc. For our purpose, we take the following definition:

Some examples will help. Consider the curves \(E : y^2 = x^3 + x\) and \(E’ : y^2 = x^3 - 4x\) over some arbitrary field \(K\). There is an isogeny \(\varphi : E \to E’\) between them, given by \(\varphi_1(x, y) = \left(\frac{x^2 + 1}{x}, \frac{x^2y - y}{x^2}\right)\). Let’s verify the properties above! This is a valid map onto \(E’\), which can be checked via direct substitution. The isogeny is a rational map with denominators \(x\) and \(x^2\), which means that when \(x = 0\), we get \(\varphi_1(x, y) = \mathcal{O}_{E’}\), the point at infinity (and also the identity element). There are only finitely many solutions to \(x = 0\) on \(E\) (in fact, just \((0, 0)\)), so \(\varphi_1\) indeed has finite kernel. As a consequence, the isogeny is not injective and hence does not have an inverse. However, there still exists a “close enough” solution, called the dual isogeny and denoted \(\widehat{\varphi_1} : E’ \to E\). In our case, it is given by \(\widehat{\varphi_1}(x, y) = \left(\frac{x^2 - 4}{4x}, \frac{(x^2 + 4)y}{8x^2}\right)\). We will investigate dual isogenies in future posts, but for now, we only need to know that an isogeny in the opposite direction exists. This means we can say two curves are isogenous when there is an isogeny between them without ambiguity.

Over finite fields, there are more isogenies from \(E\). For example, there is an isogeny from \(E\) to \(E’ : y^2 = x^3 + 6x + 3\) over \(K = \mathbb{F}_{17}\), given by \(\varphi_2(x, y) = \left(\frac{13x^2 + 16x + 8}{x + 13}, \cdots\right)\), and similarly there is a dual isogeny from \(E’ \to E\), given by \(\widehat{\varphi_2}(x, y) = \left(\frac{x^2 + 2x + 1}{x + 2}, \cdots\right)\). For both examples, we say \(E\) and \(E’\) are isogenous. The curve \(E\) is the domain and the curve \(E’\) is the codomain. We will investigate the relations between \(\varphi\) and \(\widehat{\varphi}\) in the next isogeny post.

There is also a special type of isogeny that exists for all elliptic curve \(E\), which is the map \([k] : P \mapsto [k]P\). It is a group homomorphism and has finite kernel Since the group law is a rational map, though one has to prove it doesn’t vanish. , and so it is an isogeny for all integer \(k \in \Z\). It maps \(E\) to itself, so we give it a special name, called an endomorphism. These endomorphisms will be very important in a few posts.

Finally, just to be clear, not all elliptic curves are isogenous. By a consequence of Tate’s isogeny theorem, two elliptic curves over a finite field are isogenous if and only if they have the same number of points. Hence, for example, \(E : y^2 = x^3 + x\) and \(E’ : y^2 = x^3 + x + 1\) are not isogenous over \(\mathbb{F}_{10^9 + 7}\), because one has order \(10^9 + 8\) and one has order \(10^9 - 46994\). We will see a way to figure out which is which easily later in this post.

Studying Isogenies

As mentioned, isogenies are group homomorphisms, so we would like to understand the complicated isogenies above by connecting them to group theory. To do so, we introduce the following theorem, taken from AEC, Proposition III.4.12. It will be extremely important throughout the remaining posts. It black-boxes many machineries and allows us to focus on the important bits and building intuitions.

The notation \(E / G\) simply denotes the image of \(E\) under the isogeny with kernel \(G\). In particular, it is not a quotient group construction! As we saw before, \(E / G\) are separate curves from \(E\), not even a subgroup. Clearly, an isogeny \(\varphi_P\) also uniquely defines its kernel \(\ker(\varphi_P)\), so there is a bijection between finite subgroups and isogenies. Moreover, given the kernel subgroup \(G\) as a list of points, Vélu’s formula allows us to compute the codomain \(E’ = E / G\) in time \(\mathrm{poly}(|G|)\). In the cyclic case, we can compute \(E / \langle P \rangle\) in time \(\mathrm{poly}(\mathrm{ord}(P))\).

As noted before, isogenies are not isomorphisms. Indeed, the isogeny \(\varphi : E \to E / \langle P \rangle\) has kernel \(\langle P \rangle\), \(\varphi_1\) has kernel \(\{O, (0, 0)\}\), etc. We define the degree of \(\varphi\) to be \(\deg(\varphi) \coloneqq |\ker(\varphi)|\). For example, \(\deg(\varphi) = |\langle P \rangle| = \mathrm{ord}(P)\), \(\deg(\widehat{\varphi}) = 2\), etc. One important case is the scalar endomorphisms \([k]\) with degrees \(k^2\) - even if \(K\) is not algebraically closed. The reason is that there are \(k^2\) points of order dividing \(k\) in general on \(E\) (over an algebraically closed field), a fact that we will use later.

Next, we need to define a “hard” problem. In RSA we had the factorisation problem, in elliptic curve cryptography we had the discrete logarithm problem, and in isogeny-based cryptography one of the hard problems is the isogeny path problem.

There are other variants of this problem, such as finding an isogeny of specified degree, of smooth degree, etc., and we shall see an example later.

Supersingular Isogeny Diffie-Hellman (SIDH)

Surprisingly, we already have enough tools to construct an isogeny based key exchange using the Diffie-Hellman idea, called the Supersingular Isogeny Diffie-Hellman (SIDH) protocol. Let’s fix a public starting elliptic curve \(E_0\), and let the two parties in the key exchange be \(A\) and \(B\). The idea is as follows: they each choose a random point \(P\) and \(Q\) respectively, and compute the targetting curve \(E_A \coloneqq E_0 / \langle P \rangle\) and \(E_B \coloneqq E_0 / \langle Q \rangle\) respectively. Then, they exchange the curves, and compute the curve \(E_0 / \langle P, Q \rangle ``= E_A / \langle Q \rangle = E_B / \langle P \rangle’’\), to complete the following diagram. This is an adaptation of the group-based Diffie-Hellman, where instead of computing \(g \mapsto g^a\) one computes \(E \mapsto E / \langle P \rangle\).

However, there is a catch. The point \(P\) doesn’t even lie on \(E_B\)! How do we “translate” the blue arrow from \(E_0 \to E_A\) onto \(E_B\) i.e. how do we compute \(E_B / \langle P \rangle\)? The idea is simple: instead of taking the isogeny with kernel \(\langle P \rangle\) at \(E_B\), we use the pushforward I don’t think this is the correct terminology, but it’s what I imagine in my head, and it makes sense on a diagram too. \(\varphi_B(P)\) as the kernel instead. Then, party \(A\) can compute by \(E_{AB} = E_B / \langle \varphi_B(P) \rangle = (E_0 / \langle Q \rangle) / \langle \varphi_B(P) \rangle\). The correctness proof is purely group theoretic.

Still, this cannot be a cryptographic protocol, since party \(A\) doesn’t know \(\varphi_B\) and thus cannot compute \(\varphi_B(P)\) by themselves. To resolve this, we require the following theorem about the group structure of torsion points on \(A\), taken from AEC, Corollary III.6.4:

In other words, when considering \(E\) over the algebraically closed finite field, there exists a basis \(\{R_1, R_2\}\) such that every point in \(E[m]\) is a integer combination of \(R_1\) and \(R_2\). Let’s now apply this to our protocol. For simplicity sake, we only worry about party \(A\) with their points \(P\). First, we fix the order of \(P\) and a public basis \(P_1, P_2\) of \(E[\mathrm{ord}(P)]\). Then, instead of choosing a random point of order \(\mathrm{ord}(P)\), party \(A\) can instead choose two integers \(0 \leq a_1, a_2 < m\), and compute \(P = [a_1]P_1 + [a_2]P_2\). To resolve our original problem of computing \(\varphi_B(P)\), we can make party \(B\) send the pushforward images \(\varphi_B(P_1)\) and \(\varphi_B(P_2)\). By the homomorphism property, we will have \(\varphi_B(P) = [a_1]\varphi_B(P_1) + [a_2]\varphi_B(P_2)\). This step will be explained more clearly at the end of this post with pseudocode.

We now proceed to choose the parameters. To begin, the orders of \(P\) and \(Q\) cannot be too small, or otherwise, we can just bruteforce all points on \(E_0\) with that order. However, it also cannot be too large. Recall that Vélu’s formula runs in time polynomial in \(\mathrm{ord}(P)\). What can we do?

There is an elegant solution: Instead of computing a single isogeny, we decompose it into an isogeny chain. An isogeny chain is simply a chain of compatible isogenies \(\varphi_1 : E_0 \to E_1, \varphi_2 : E_1 \to E_2, \ldots, \varphi_k : E_{k - 1} \to E_k\), and by decomposing an isogeny we mean writing \(\varphi = \varphi_k \circ \cdots \circ \varphi_1\). There are various properties of such chains, but one important one is that \(\deg(\varphi) = \deg(\varphi_1) \cdots \deg(\varphi_k)\) (this can be proven by looking at the kernels, again as group homomorphisms).

In our case, we can take \(P\) to be a random point of order \(2^a\) for some integer \(a\). Our task now becomes decomposing the isogeny \(\varphi_A : E_0 \to E_0 / \langle P \rangle\). By definition, \(\langle P \rangle = \{O, P, 2P, \cdots, (2^a - 1)P\}\). We can see that it is made out of many layers. For example, we can first split the subgroup into two halves, i.e. \(\langle P \rangle = \{O, P, 2P, \cdots, (2^{a - 1} - 1)P\} \oplus \color{pink}{\{0, 2^{a - 1} P\}}\). Then, \(E_0 / \langle P \rangle = \color{pink}{(E_0 / \langle 2^{a - 1} P \rangle)} / \{O, P, 2P, \cdots, (2^{a - 1} - 1)P\}\), where \(\color{pink}{\langle 2^{a - 1} P \rangle}\) is the outermost “layer”. Repeating this process, one can see that we have the following decomposition:

Similarly, we can also take \(Q\) to be a random point of order \(3^b\) for some integer \(b\), and a similar isogeny chain can be used to compute the codomain \(E / \langle Q \rangle\). In the SIDHp434 parameter set, the parameters \(a = 216\) and \(b = 137\) are taken. For our purpose, we will play around with a smaller parameter set \((a, b) = (91, 57)\) instead.

This then brings us into the next problem, which is that such points \(P\) and \(Q\) may not exist! To ensure that points of order \(2^a\) and \(3^b\) to exists, \(2^a 3^b\) must divide \(|E|\). One option is to try random elliptic curves \(E\) over random finite fields \(K\), compute the curve’s order using an efficient algorithm (such as the Schoof-Elkies-Atkin Algorithm), and test if the property holds. However, this is clearly infeasible for cryptographic parameters like \(a = 216\) and \(b = 137\). This brings us into the S in SIDH.

Supersingular Elliptic Curves

Although all elliptic curves are equal, some are more equal than others. As it turns out, elliptic curves can be divided into two classes, the ordinary ones and the supersingular ones. There are many equivalent characterisations of supersingular elliptic curves, but here is one of them.

As it is, the definition is quite arbitrary. However, we have the following powerful lemma:

How does this help us? Well, if we take \(k = 2\), then we see that as long as \(E\) is defined over \(\mathbb{F}_p\), then \(|E(\mathbb{F}_{p^2})| = (p + 1)^2\). Recall that we need \(2^a 3^b\) to divide \(|E(K)|\) in order to make the point selection in the protocol work. This is simple, as we can pick a (small) integer \(f\) such that \(p = f \cdot 2^a 3^b - 1\) is a prime, and use \(\mathbb{F}_{p^2}\) as our base field

We only have one task left now, namely to construct a supersingular elliptic curve over \(\mathbb{F}_p\). To do so, (maybe you see the pattern,) we simply refer to the book again: AEC, Example V.4.5 shows that the curve \(E: y^2 = x^3 + x\) is supersingular over \(\mathbb{F}_{p^k}\) when \(p \equiv 3 \pmod{4}\). Hence, we can initialise our scheme with this curve. And… we’re done!

Cryptographic Assumptions

Let’s briefly think about what SIDH actually relies on as its hardness assumption. We observe that it relies on a weaker version of isogeny path problem: given \(E_0, E_A, E_B\) and the four pushforward images, if a malicious party can find an isogeny between \(E_0\) and \(E_A\), then \(E_{AB}\) can be found already. This is a weakened version since we are given extra information (namely the pushforward images, or the torsion information).

Detailed Protocol

Okay, so I yapped a bunch of random stuff, but what does the protocol actually look like? Here is a rough outline for a SIDH key exchange between Alice (he/him) and Bob (she/her) with our toy parameters.

Public Parameters:

• Integers \(a = 91, b = 57, f = 1\), so \(p = 2^{91} \cdot 3^{57} - 1\)
• Supersingular elliptic curve \(E_0 : y^2 = x^3 + x\) over a fixed A modulus should be chosen. We will use \(x^2 + 1\) here, i.e. \(\mathbb{F}_{p^2} \cong \mathbb{F}_p[X] / (X^2 + 1)\) \(\mathbb{F}_{p^2}\)
• basis \(\color{pink} \{P_1, P_2\}\) of \(E_0[2^a]\)
• basis \(\color{lime} \{Q_1, Q_2\}\) of \(E_0[3^b]\)

Private Keys:

• Alice: Random integers \(a_1, a_2\)
• Bob: Random integers \(b_1, b_2\)

Key Exchange:

• 0A. Alice computes \(P = [a_1]P_1 + [a_2]P_2 \in E_0\)
• 1A. Alice computes \(\varphi_A : E_0 \to E_A\) with \(E_A = E_0 / \langle P \rangle\)
• 2A. Alice computes \(Q_1’ = \varphi_A(Q_1)\) and \(Q_2’ = \varphi_A(Q_2)\)
• 0B. Bob computes \(Q = [b_1]Q_1 + [b_2]Q_2 \in E_0\)
• 1B. Bob computes \(\varphi_B : E_0 \to E_B\) with \(E_B = E_0 / \langle Q \rangle\)
• 2B. Bob computes \(P_1’ = \varphi_B(P_1)\) and \(P_2’ = \varphi_B(P_2)\)

• 3A. Alice sends \(E_A\), \(Q_1’\) and \(Q_2’\) to Bob
• 3B. Bob sends \(E_B\), \(P_1’\) and \(P_2’\) to Alice

• 4A. Alice computes \(P’ = [a_1]P_1’ + [a_2]P_2’ \in E_B\)
• 5A. Alice computes \(\color{gold} E_{AB} = E_B / \langle P’ \rangle\)
• 4B. Bob computes \(Q’ = [b_1]Q_1’ + [b_2]Q_2’ \in E_A\)
• 5B. Bob computes \(\color{gold} E_{BA} = E_A / \langle Q’ \rangle\)

Alice and Bob have now successfully obtained a shared secret \(\color{gold} E_{AB} = E_{BA}\)… not exactly. I have glossed over many details in this post, but one of them is that \(\color{gold} E_{AB}\) is only isomorphic to \(\color{gold} E_{BA}\). Hence, in the SIDH protocol, one computes an invariant (with respect to isomorphisms) of the elliptic curves, e.g. the \(j\)-invariant. We shall investigate this further in the next post, where we implement this scheme.

Remark

Oh yeah, SIDH is broken in 2022 by Castryck-Decru and others. Don’t use it.

For no reason, here’s a song I like recently.