Blog by grhkm

Learning Without Errors (396 pts, 6 solves, upsolve)

(Up-)Solved by: grhkm

Source of the problem: Dice CTF 2022

Self-Reflection

I am actually very frustrated and annoyed at myself for this problem. During the CTF I was scared off by my lack of experience with this encryption scheme, and also just didn’t believe I can solve this challenge. As a result, I spent a lot of my time watching YouTube instead.

Approaching the end of the CTF, for absolutely no reason I decided I will try to take a look at the challenge. I started the biggest crossover between the CTF and the speed-running community ever and seriously attempted the challenge in the last hour and half of the CTF. I watched a video on Homomorphic Encryption while I ate dinner, and an hour before the end of CTF I found the correct paper and started tracing the given fhe library. At the end I had the idea of the solution and was ready to start coding. But of course, it was also the end of CTF! After the contest, I finished coding my solution in around an hour, while debugging took me around 3 hours, mainly due to my unfamiliarity with the system. Nonetheless, I would have solved this if not due to my lack of confidence and if I actually spent time on this crypto challenge, which I am meant to excel in…

Problem Statement

Choose Keys Karefully for Security

nc mc.ax 31614

server.py

challenge.py

Solution Outline

The ciphertext-message pair leaks the secret key as a linear equation, and we can simply decrypt the flag. Yes, it’s that simple.

Understanding the Code

Let’s first try to understand the flow of the challenge by looking at server.py:

from challenge import Challenge

poly_degree = 1024
ciph_modulus = 1 << 100

print('Please hold, generating keys...', flush=True)
chal = Challenge(poly_degree, ciph_modulus)
print('Welcome to the Encryption-As-A-Service Provider of the Future, powered by the latest in Fully-Homomorphic Encryption!')

data = input('Provide your complex vector as json to be encrypted: ')
data = json.loads(data)

ciph = chal.encrypt_json(data)
string_ciph = json.dumps(chal.dump_ciphertext(ciph))
print('Encryption successful, here is your ciphertext:', string_ciph)

plain = chal.decrypt_ciphertext(ciph)
string_plain = json.dumps(chal.dump_plaintext(plain))
print('To verify that the encryption worked, here is the corresponding decryption:', string_plain)

e_flag = chal.encrypt_flag()
string_flag = json.dumps(chal.dump_ciphertext(e_flag))
print('All done, here\'s an encrypted flag as a reward:', string_flag)

print('Enjoy DiceCTF!')

The cryptography-related functions are implemented in challenge.py instead.

In other words, we have to perform a Single Chosen Plaintext attack. Let’s now take a look at challenge.py. Note that the script uses an external implementation of CKKS, which can be found at sarojaerabelli/py-fhe. I will refer to it as “the library” from now on.

# https://github.com/sarojaerabelli/py-fhe
# imports omitted

class Challenge:
    def __init__(self, poly_degree, ciph_modulus):
        big_modulus = ciph_modulus**2
        scaling_factor = 1 << 30

        params = CKKSParameters(poly_degree=poly_degree,
                                ciph_modulus=ciph_modulus,
                                big_modulus=big_modulus,
                                scaling_factor=scaling_factor)

        key_generator = CKKSKeyGenerator(params)
        public_key = key_generator.public_key
        secret_key = key_generator.secret_key
        encoder = CKKSEncoder(params)
        encryptor = CKKSEncryptor(params, public_key, secret_key)
        decryptor = CKKSDecryptor(params, secret_key)
        evaluator = CKKSEvaluator(params)

        # irrelevant code omitted

    def encrypt_flag(self):
        with open("flag.txt", "rb") as f:
            flag = f.read()

        n = self.poly_degree // 2

        flag = int.from_bytes(flag, "big")
        flag = f"{flag:0{n}b}"
        flag = [float(i) for i in flag]

        d = {"real_part": flag, "imag_part": [0] * n}
        ciph = self.encrypt_json(d)
        return ciph

    def dump_ciphertext(self, ciph):
        d = {"c0" : ciph.c0.coeffs,
             "c1" : ciph.c1.coeffs,
             "poly_degree" : ciph.c0.ring_degree,
             "modulus" : ciph.modulus}
        return d

    def dump_plaintext(self, plain):
        d = {"m" : plain.poly.coeffs,
             "poly_degree" : plain.poly.ring_degree,
             "scaling_factor" : plain.scaling_factor}
        return d

    def dump_decoded_plaintext(self, plain):
        x = [complex(i) for i in plain]
        real = [i.real for i in plain]
        imag = [i.imag for i in plain]
        d = {"real_part": real, "imag_part": imag}
        return d

    def decrypt_ciphertext(self, ciph):
        plain = self.decryptor.decrypt(ciph)
        return plain

    def decrypt_and_decode_ciphertext(self, ciph):
        plain = self.decryptor.decrypt(ciph)
        plain = self.encoder.decode(plain)
        return plain

    def encrypt_json(self, d):
        real = list(d["real_part"])
        imag = list(d["imag_part"])

        message = [r + 1j * i for r,i in zip(real, imag)]
        assert len(message) == self.poly_degree // 2

        plain = self.encoder.encode(message, self.scaling_factor)
        ciph = self.encryptor.encrypt(plain)
        return ciph

There are quite a few functions to keep track of here. Here I highlight the library function calls.

With this noted, let’s try to solve the challenge. Before we do that, of course we have to know: what is CKKS???

Fully Homomorphic Encryption (FHE)

To motivate the idea of Fully Homomorphic Encryption (FHE), imagine that you have two secret prime numbers (your crush’s phone number and birthday!), $m_1$ and $m_2$, that you want to store in a secure cloud server. Obviously you should not trust the cloud, so you encrypted them as $c_1 := \text{enc}_{\text{pk}}(m_1)$ and $c_2 := \text{enc}_{\text{pk}}(m_2)$, and stored it into the cloud. Now suppose that you want to merge them together, which involves calculating $m_3 = m_1 \cdot m_2$. Of course, one way to do this is to decrypt both the messages, multiply them together, then encrypt and store it back. However, the cloud might intercept the decrypted messages, which is bad.

Here is when FHE will help - FHE allows you to calculate $c_3 = \text{enc}_{\text{pk}}(m_3)$ directly without knowing $m_1$ and $m_2$. In particular, there are operators $\oplus$ and $\otimes$ such that

$$\begin{align*} \text{enc}{\text{pk}}(m_1)\ {\color{red}\oplus}\ \text{enc}{\text{pk}}(m_2) &= \text{enc}{\text{pk}}(m_1\ {\color{cyan}+}\ m_2) \\ \text{enc}{\text{pk}}(m_1)\ {\color{red}\otimes}\ \text{enc}{\text{pk}}(m_2) &= \text{enc}{\text{pk}}(m_1\ {\color{cyan}\cdot}\ m_2) \end{align*}$$

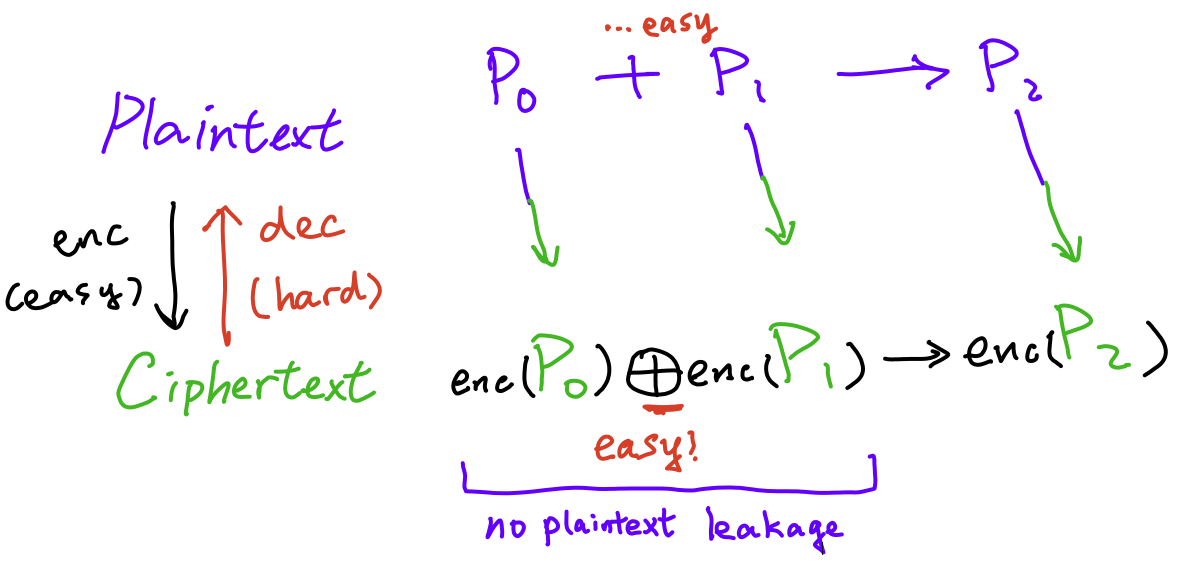
Here, “easy” and “hard” is from the perspective of the cloud. It is easy to go right and down, but not up.

In other words, it allows one to perform computations over encrypted data without ever decrypting them. Notice the parallel between the plaintext space and the ciphertext space! This is why it is called a homomorphic scheme. This property is very useful and has practical uses, most importantly in cloud computing. I shall refer the reader to watch the first half of this podcast, which explains the concept in layman terms, and this Eurocrypt 2019 talk, which is a pretty clear talk.

CKKS (Cheon-Kim-Kim-Song) Scheme

The CKKS Encryption Scheme, named after Jung Hee Cheon, Andrey Kim, Miran Kim and Yongsoo Song, is a Fully Homomorphic Encryption (FHE) scheme proposed in 2016 that’s based on approximate arithmetic. The core idea comes from the difficulty of Learning With Errors (LWE), that is, the difficulty of recovering the secret key $\vec{s}$ given only “approximate” random linear equations on $\vec{s}$. For example, it is hard to recover $\vec{s}$ given equations

$$\vec{b_i} = \vec{a_i}\cdot\vec{s} + \vec{e_i} \approx \vec{a_i}\cdot\vec{s}$$

Where $\vec{e_i}$ is the error term sampled from a secure error distribution $\chi$, usually chosen to be the normal distribution.

The scheme is fascinating and has a lot of details, but I will provide a simplified outline of the scheme to ease understanding. Hence, details such as scaling factors and relinearization will be left out. Interested readers shall refer to the original paper (linked) or [BD21, p.8].

Data Representation

In the scheme, all operations are done with real polynomials of degree $\leq N$, where the coefficients are taken mod $q$. Our plaintext would be a complex vector, chosen as the evaluation of the polynomial at the primitive $(2N)$th roots of unity $\zeta^{2j + 1}$ for a few reasons.

First, notice that as these are primitive roots, they satisfy $x^N + 1 = 0$. This means that our polynomial can be reduced mod $x^N + 1$ and not affect the decoded vector, which means we can compute polynomial operations mod $x^N + 1$.

Furthermore, since we have $\zeta^{2j + 1} = \overline{\zeta^{-2j - 1}}$ as conjugate pairs and that our polynomial has real coefficients, we essentially get duplicate information: $P(\overline{x}) = \overline{P(x)}$. Hence, the scheme drops half of the roots of unity without losing information bits.

Finally, evaluation at roots of unity just screams FFT, which will greatly accelerate the calculations! From all this, we arrive at the following decoding function $\phi$:

$$\begin{align*} &\mathcal{O} := \left(\mathbb{Z} / q\mathbb{Z}\right)[x] / (x^N + 1) \cong \left(\mathbb{Z} / q\mathbb{Z}\right)^N \\ &\phi : \mathcal{O} \to \mathbb{C}^{\frac{N}{2}} \\ &\phi(a(x)) \to \tilde{a} = \left(a(\zeta^{4j + 1})\right)_{j=0}^{\frac{N}{2} - 1} \end{align*}$$

Where the final expression is simply a vector of the valuation results. The encoding function is then simply $\phi^{-1}$. This is all implemented in the py-fhe library and can be done in sub-$O(N^2)$ time via FFT.

Key Generation

Obviously, the scheme requires a public key and a secret key. In the actual CKKS scheme, there are also switching keys and relinearization keys, which I think will only further confuse matters and hence will be omitted.

Firstly, we choose an error distribution $\chi$ and a secret distribution $\chi’$. As mentioned, the scheme is proven to be secure for normal distributions $\chi$ and $\chi’$. However, for efficiency reasons, simpler distributions are chosen for the scheme. Here, the error distribution is

$$\chi = \{-1, 0, 1\}^n$$

Where for each of the $n$ entries, $-1, 0, 1$ have probability $25\%, 50\%$ and $25\%$ respectively. On the other hand, the secret distribution $\chi_h’$ is

$$\chi_h’ = \{\vec{s} \in \{0, \pm 1\}^n : \sum_{i=1}^n |s_i| = h\}$$

i.e. the set of signed binary vectors where the hamming weight is exactly $h$, and each term has equal probability.

Let’s write $a \gets \chi$ to mean “sample the variable $a$ from $\chi$”. From here, it is easy to describe our keys:

Encryption

The encryption algorithm $\text{enc}_{\text{pk}}(m)$ is also simple:

Approximated Decryption

The approximated decryption algorithm $\text{dec}_{\text{sk}}(\text{ct})$ is even simpler:

Notice how it’s called approximated decryption. This is because expanding the calculation by decrypting the encrypted results, we have

$$\begin{align*} m &\approx c_1 + sc_2 \\ &= (m + p_1u + e_1) + s(p_2u + e_2) \\ &= (m + e_1 + se_2) + \underbrace{(-as + e)}{p_1}u + \underbrace{a}{p_2}su \\ &= m + (e_1 + se_2 + eu) \mod q \end{align*}$$

However, $e_1 + se_2 + eu$ is small, as $e, e_1, e_2$ and $u$ are all chosen from $\chi$ which gives small polynomials. Therefore, the decrypted results are “close enough” to the original message.

Hidden in Plain Sight

Phew. That was a lot of maths to unpack. However, it is a lot easier from here.

Looking back at our challenge, we are able to supply $m$ and receive

$$\begin{align*} \text{enc}_{\text{pk}}(m) &= (c_1, c_2) = \ldots \\ \text{dec}_{sk}(\text{enc}_{pk}(m)) &= c_1 + sc_2 = \ldots \\ \text{enc}_{\text{pk}}(flag) &= \ldots\end{align*}$$

Wait… this means that we are given $c_1, c_2, c_1 + sc_2$. Of course, we can recover $s$! Our $m$ doesn’t even matter. Let’s code this up and see:

import json
from pwn import *

q = 1 << 100 # ciph_modulus
N = 1024 # poly_degree

r = remote('mc.ax', 31614)

# receive our data
zeros = [float(0.0)] * (N // 2)
r.recvuntil(b'to be encrypted: ')
r.sendline(json.dumps({"real_part": zeros, "imag_part": zeros}).encode())

ct = eval(r.recvline().decode().strip().split('ciphertext: ')[1])
msg = eval(r.recvline().decode().strip().split('decryption: ')[1])
flag = eval(r.recvline().decode().strip().split('reward: ')[1])

# these are coefficients of the actual polynomials
msg_c0, msg_c1, msg_dec = ct['c0'], ct['c1'], msg['m']
flag_c0, flag_c1 = flag['c0'], flag['c1']

# convert to our polynomials
R.<x> = PolynomialRing(Zmod(q), 'x').quotient(x^N + 1)
to_poly = lambda arr: sum(arr[i] * x^i for i in range(len(arr)))
msg_c0, msg_c1, msg_dec, flag_c0, flag_c1 = map(to_poly, [msg_c0, msg_c1, msg_dec, flag_c0, flag_c1])

# as derived, msg_dec = msg_c0 + secret * msg_c1
secret = (msg_dec - msg_c0) / msg_c1
print(secret)

Output:

NotImplementedError: The base ring (=Ring of integers modulo 1267650600228229401496703205376) is not a field

Fuck sage <3

Problem 1: Can’t invert

As shown by the error, Sage is not able to compute the inverse of msg_c1, required to divide, since $\mathbb{Z} / q\mathbb{Z}$ is not a field. For example, $2$ does not have an inverse $\mod q$, since $q = 2^{100}$. However, some elements are still invertible, and Sage is not able to calculate them. We can attempt to implement our own division instead of using Sage’s,

# ax + by = 1
def xgcd(a, b):
    if b == 0:
        return 1, 1, 0
    g, x, y = xgcd(b, a % b) # fill in the blanks
    return g, y - (b // a) * x, x

def inverse(a, b):
    return xgcd(a, b)[1]

However, the algorithm still requires division, which is not always possible. We need a better way…

Fix 1: Use Gareth T.(heorem)

As we mentioned, $2$ does not have an inverse $\mod q$. However, it is easy to see that all odd numbers $n = 2k + 1$ has an inverse. Let’s look the inverse:

$$\frac{1}{n} = \frac{1}{1 + 2k} \stackrel{?}{=} \sum_{i=0}^{\infty} (-2k)^i\mod 2^{100}$$

Where the last (in)equality follows from a geometric series expansion. Now, notice that $(-2)^{-i}$ is actually eventually non-zero modulo $2^{100}$! In particular, we only have to sum the first $99$ terms of the series:

$$\frac{1}{1 + 2k} \equiv \sum_{i=0}^{99} (-2k)^{i}\mod 2^{100}$$

One can prove this by copying the proof of geometric series - multiply by $(-2k)$, subtract and divide. However, I prefer a better method: Prove by AC.

while True:
    k = randint(0, q // 2) * 2
    assert sum(pow(-k, -i, q) for i in range(100)) * (1 + k) == 1

Now, we can try to apply this for invertible polynomials in general. It is not hard to prove that polynomials are only invertible if their constant term is odd. For such polynomials, we can write $P(x) = c_0P_1(x) = c_0(1 + Q(x))$, where $c_0$ is the constant term. Then,

$$\begin{align*} \frac{1}{P(x)} &= \frac{1}{c_0}\cdot\frac{1}{1 + Q(x)} \ &\equiv c_0^{-1}\sum_{i=0}^{\infty} (-Q(x))^i \mod (x^N + 1) \end{align*}$$

However, it turns out that this method doesn’t always converge for all invertible polynomials - in fact, it converges for about 50% of the time, and a proof is included at the end. Moreover, the theoretical upper-bound for the converging $j$ is $2^{111}$, which would be impossible to compute with the $O(j)$ series. However, numerical evidence shows that $j$ is usually smaller. For reference, $j\leq 2^{15}$ for about 3% of the cases, and $j\leq 2^{16}$ for about 13%. (Keep in mind that it is polynomial arithmetic, and I am lazy to implement FFT). Therefore, we can assume that $j = 2^{16}$ is an upper bound and simply binary search for it.

# notice we change the definition to without quotient
R.<x> = PolynomialRing(Zmod(q), 'x')

def inverse(a):
    c0 = a[0]
    assert c0 % 2 == 1

    # Q is the geometric series ratio
    a /= c0
    Q = a - 1

    # find bounds
    assert pow(Q, 2^32, x^N + 1) == 0
    upper = 2^32
    lower = 0
    result = -1
    while upper >= lower:
        mid = (lower + upper) // 2
        if pow(-Q, mid, x^N + 1) == 0:
            result = mid
            upper = mid - 1
        else:
            lower = mid + 1

    # sum and return
    total = 0
    cur =  1
    for i in tqdm(range(result)):
        total += cur
        cur = cur * -Q % (x^N + 1)
    return total / Mod(c0, q)

Run it on inverse(R(3)), and

------------------------------------------------------------------------
(no backtrace available)
------------------------------------------------------------------------
Unhandled SIGABRT: An abort() occurred.
This probably occurred because a *compiled* module has a bug
in it and is not properly wrapped with sig_on(), sig_off().
Python will now terminate.
------------------------------------------------------------------------
/usr/local/bin/sage: line 19: 51248 Abort trap: 6           "$SYMLINK/local/bin/sage" "$@"

???????

Bug 2: Sage, What’s Wrong With You?

To this day, I still have no idea why pow fails even with int exponents. I discovered this code in polynomial_modn_dense_ntl.pyx, but… ?:

if not isinstance(modulus, Polynomial_dense_modn_ntl_ZZ):
    modulus = self.parent()._coerce_(modulus)
ZZ_pX_Modulus_build(mod[0], (<Polynomial_dense_modn_ntl_ZZ>modulus).x)

do_sig = ZZ_pX_deg(self.x) * e * self.c.p_bits > 1e5
if do_sig: sig_on()
ZZ_pX_PowerMod_long_pre(r.x, self.x, e, mod[0])
if do_sig: sig_off()

Anyways, the fix for this is pretty simple.

Fix 2: Take Matters Into My Own Hands

Since Sage refuses work and never works, I wrote my own pow implementation:

def qpow(a, b, m):
    res = 1
    while b > 0:
        if b & 1:
            res = res * a % m
        a = a * a % m
        b >>= 1
    return res

Final Step

With this, our code finally runs, at least 50% of the time (due to the polynomial being invertible 50% of the time). It takes a while, but after we recover the secret, we can compute the decrypted flag and decode for the flag.

[INFO] 李家超提提你

Can’t be me who forgot to decode the flag and spent 1.5 hours trying to figure this out. Remember this?

Relevant code:

# setup secret key, mapping q - 1 to -1
coef = list(map(ZZ, secret.coefficients(sparse=False)))
while len(coef) < N:
    coef.append(0)
for i in range(N):
    if coef[i] == q - 1:
        coef[i] = -1
secret = SecretKey(Polynomial(N, coef))

# decoder
big_modulus = q ** 2
scaling_factor = 1 << 30
params = CKKSParameters(
    poly_degree=N,
    ciph_modulus=q,
    big_modulus=big_modulus,
    scaling_factor=scaling_factor,
)

# use py-fhe library
decryptor = CKKSDecryptor(params, secret)
flag_c0 = Polynomial(N, flag_c0.coefficients(sparse=False))
flag_c1 = Polynomial(N, flag_c1.coefficients(sparse=False))
flag = decryptor.decrypt(Ciphertext(flag_c0, flag_c1, scaling_factor=scaling_factor, modulus=q))

encoder = CKKSEncoder(params)
flag = encoder.decode(flag)

flag = ''.join(map(str, [round(r.real()) for r in arr]))
flag = bytes.fromhex('{:64x}'.format(flag))
print(f"Flag: {flag.decode()}")

With all this done, we simply have to run our script, extract the real part of each complex number, and get the flag~

Flag: dice{this_destroyes_the_CKKS_cryptosystem_a3b31e683b82b26f}

Thank you for reading this blog, and thank you to @ireland for the challenge. Also thank you @Mystiz for suggesting the title “Gareth T”, it’s a singer in Hong Kong :D Still wish I solved this during the CTF though :3

Thank you for reading!
Thank you for reading!

Appendix: Proof

Below, I will prove that for $N = 2^{10}$ and $q = 2^{100}$, as it is in the scheme, then

$$P(x)\equiv 0\mod (2, x + 1)\implies \lim_{n\to\infty} P(x)^{2^n}\equiv 0\mod (q, x^N + 1).$$

In other words, our geometric series converges if $(x + 1)$ is a factor of $P(x)$ mod $2$. Thank you @jschnei for the proof idea!

Proof:

If $(x + 1)\mid P(x)\mod 2$, then we can write $P(x) = (x + 1)Q(x)$. By Freshman’s Dream, we know that

$$(x + 1)^N\equiv x^N + 1\mod 2.$$

Raising this to the $100^{\text{th}}$ power, we have

$$\begin{align*} (x + 1)^{100N}&\equiv (x^N + 1)^{100} &\mod q \\ (x + 1)^{100N} &\equiv 0 &\mod (q, x^N + 1) \end{align*}$$

Therefore, $P(x)^{100N} = P(x)^{102400}$ will converge to $0$.

It is not clear what happens when $(x + 1)$ is not a divisor of $P(x)$.

Update: Woohoo! @jschnei is back with another update! Thank you once again.

Apparently, having an even constant term in the polynomial doesn’t mean we can’t invert the polynomial. Example? $x^{1024} + 2$.

Motivated by this, we simply consider $P(x) + (x^{1024} + 1)$ if the constant term is even, and if $(x + 1)\mid P(x)$, then $(x + 1)\mid P(x) + (x^{1024} + 1)$ by factor theorem and we proceed as above!