The Hardest Path (300 pts, 9 solves)

Source of the problem: HKCERT CTF 2021.

Summary of Problem Statement

寧願不揀最易的路 行極還未到

寧願你最後未傾慕 但信念安好

在意的 不再是 愛的煩惱

是哪樣做人 更清高

餘生那段旅途

與哪類人共舞

When you think reverse engineering is hard, try working on reverse engineering challenges > those need your algorithmic thinking skills!

nc chalp.hkcert21.pwnable.hk 28117

Attachments

• the-hardest-path_e00c6aa7b64b8dc2a06e577937b5b07c.zip

Solution Outline

We have to find a path (represented by NEWS - North, East, West, South) from source _328518a497015157 to _8b0eb6f195ae182a, which is done by constructing call relationship graph and performing shortest path algorithm (such as Dijkstra’s).

Understanding our goal

We are given two python files:

• chall.py, which is essentially a wrapper for the problem and
• lost.py, the actual code containing the logic.

# File: chall.py
# code has been rewritten

# proof of concept
challenge = os.urandom(8)
print(f'🔧 {base64.b64encode(challenge).decode()}')
response = base64.b64decode(input('🔩 '))
h = hashlib.sha256(challenge + response).digest()
return h.startswith(b'\x00\x00\x00')

# calling lost._328518a497015157(data)
try:
    data = input('🥺 ')
    lost._328518a497015157(data)
    print(os.environ.get('FLAG'))
except:
    print('no good!')

Reading chall.py, we first have to solve a proof of concept which can easily be bruteforced. We then supply the input string data and call the function _328518a497015157, which I shall refer to as src for reasons I will explain soon. The flag is returned only if the function call does not raise an Exception. That is interesting…

Understanding the logic

test.py, however, is a completely different beast. Let’s analyze the file slowly. First, we are presented with:

# File: test.py
# original
def _29aa7a86665899ed(_050ca071ab51aece): raise Exception('😵‍💫💫🧱')

# deobfuscate
def fail(_):
    raise Exception()

This function simply raises an Exception. Remember that the flag condition is for this function to not be called. Onto the next one:

# File: test.py
# original
mystery = 'NEWS'
def _f42fb5e137443877(_a78810bb76cc7d70, *_ab1bbf35017f4f42):
    def _e6aea2db2242b19f(_41d28eb8c27952c3):
        if len(_41d28eb8c27952c3) == 0:
            if not _a78810bb76cc7d70: raise Exception('🤷🏁😕')
            return
        _03d38fa3a589db14, _41d28eb8c27952c3 = _41d28eb8c27952c3[0], _41d28eb8c27952c3[1:]
        return globals()[_ab1bbf35017f4f42[mystery.index(_03d38fa3a589db14)]](_41d28eb8c27952c3) if _03d38fa3a589db14 in mystery else _e6aea2db2242b19f(_41d28eb8c27952c3)
    return _e6aea2db2242b19f

# deobfuscate (variable name change)
def process(is_end, *func_list):
    def step(arg):
        if len(arg) == 0:
            if not is_end: raise Exception('🤷🏁😕')
            return
        flag, arg = arg[0], arg[1:]
        return globals()[func_list[mystery.index(flag)]](arg) if flag in mystery else step(arg)
    return step

# deobfuscate (styling)
def process(is_end, *func_list):
    def step(arg):
        if len(arg) == 0:
            if not is_end:
                raise Exception('🤷🏁😕')
            return
        first_char, arg = arg[0], arg[1:]
        if first_char in 'NEWS':
            index = 'NEWS'.index(first_char)
            function = func_list[index]
            return eval(function)(arg)
        else:
            return step(arg)
    return step

In short, process(is_end, *func_list) returns a function which can then be called. Let’s say we call it with arg i.e. we have process(is_end, *func_list)(arg). Then there are three outcomes:

• If arg is empty, we further have
• • ✅ is_end is True: the function returns normally.
• • ❌ is_end is False: the function raises an error, causing us to lose.
• If the first character of arg is one of N, E, W, S:
• 1. We determine its index i.e. 'N' = 0, 'E' = 1, etc.
• 2. We get the function name at func_list[index] and call it with arg[1:] as a parameter.
• Otherwise, the first character is none of N, E, W, S:
• • We skip the character and move on, essentially calling process(is_end, *func_list)(arg[1:]).

If you don’t understand, reread the code and follow through with process(False, ('f1', 'f2', 'f3', 'f4'))('EW'). You should arrive at f2('W') as a result.

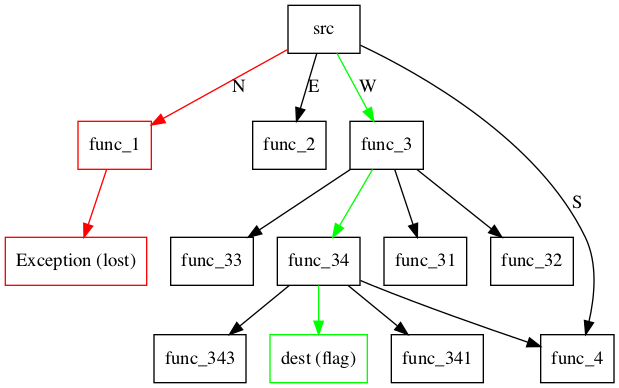
At this point, we should still have many questions, such as:

• How many arguments are there in func_list? (Well, the image is a spoiler…)
• Is there any halting condition apart from the Exception calls?
• How is this worth 300 pts?

Let’s keep these questions in mind and move on to the rest of the code.

Understanding our goal

The remaining of the code contains 40,401 lines of code, many of which seems similar. In fact, we can categorize the functions into three main categories:

• _func = fail
• _func = process(False, func1, func2, func3, func4)
• _8b0eb6f195ae182a = process(True, "_92ccf583b1b065ea", "_d3084505a4a12123", "_e335a503c47e5243", "_ebff1548ca6e8dbd")

Yes, the final one is a category on its own. That is because it is the only process function call that has is_end = True! This means that we must reach and end our function here at _8b0eb6f195ae182a, which I will call dest from now. To briefly summarize, we start from src and must supply a direction string made up of N, E, W, S, reaching the dest function at the end.

Parsing the source file

Finally, we can start solving the challenge! To begin, we will construct the adjacency list of the call graph out of the function calls in lost.py, which is a fancy way of saying “for each function _func, what are the four functions supplied into process?” In the process, we also handle when _func = fail by setting its entry to be empty, meaning it cannot reach any other node and is hence useless. Here is a short script:

import re
source = open('lost.py', 'r').read().strip().split('\n')
offset = 16  # might have to change this if you deobfuscated lost.py
call_graph = {}  # dictionary, storing {node: [reachable from node]}
src = '_328518a497015157'
dest = None

for line in source[offset:]:
    left, right = line.split(' = ')
    if right == '_29aa7a86665899ed':
        call_graph[left] = []
    else:
        if 'True' in right:
            dest = left
        # right == _f42fb5e137443877(is_flag, ...)
        funcs = re.findall(r'_[0-9a-f]{1,16}', right)[1:]
        call_graph[left] = funcs

# len(call_graph) = 40401

All there is left is to find a path from src to dest. The naive algorithm of bruteforcing all possible paths won’t work, as there are $4^{40401}$ such paths. Instead, let’s apply an algorithm called Breadth-First Search (BFS). The algorithm is very simple to understand with a few steps only:

1. Start an array queue that will store which functions to visit (“nodes”), as well as its distance.
2. Start another array visited storing which nodes we have visited.
3. Initialize our queue with (src, 0), our starting point and the distance travelled.
4. While the queue is not empty,
   4.1. Mark the first element of the queue as visited by appending it to visited.
   4.2. Push all unvisited functions reachable from it onto our queue.
   4.3. Remove the element from the queue
5. Done!

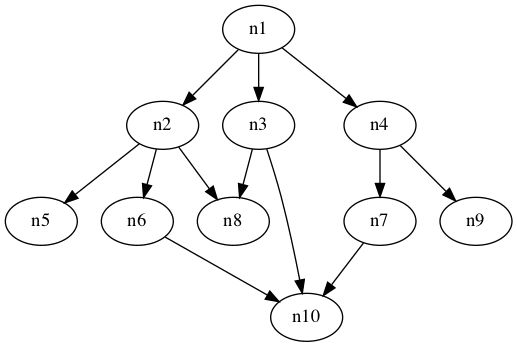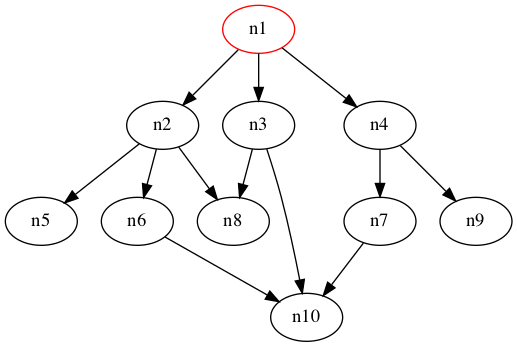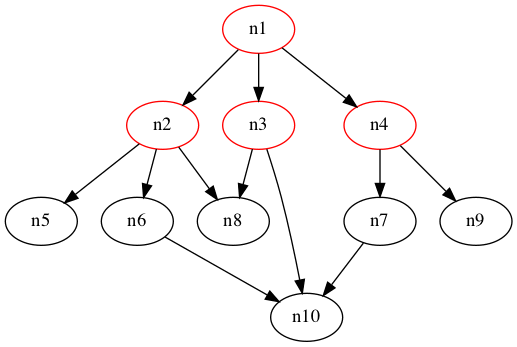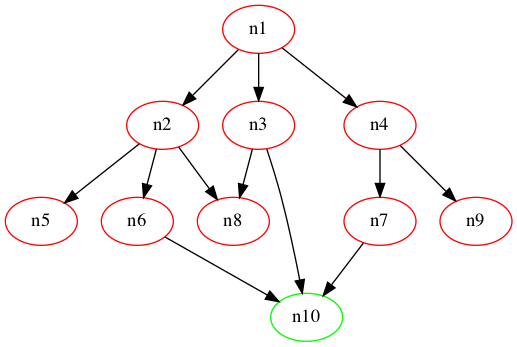
Intuitively speaking, the queue will keep track of the nodes in chronological order: the earlier the node is visited, the shorter the distance and the earlier it will be processed in (4.). You can also think of the nodes as lining up in a queue, where the earlier you arrive, the earlier you will leave! Hence, this algorithm will give us the shortest distance from src to dest, or in fact to any reachable node. Here is a simple line-by-line implementation:

queue = []                                       # 1.
visited = set()                                  # 2.
queue.append((src, 0))                           # 3.
while len(queue) > 0:                            # 4.0
    first, dist = queue[0]
    if first == dest:                            # Handle reaching dest
        print(dist)
    visited.add(first)                           # 4.1
    for reachable in call_graph[first]:
        if reachable not in visited:
            queue.append((reachable, dist + 1))  # 4.2
    del queue[0]

Running this code will print 996. Well, that’s useless! We want the full path with NEWS! Luckily, we simply store (node, path) instead of (node, dist), which is straightforward to implement:

queue = []                                          # 1.
visited = set()                                     # 2.
queue.append((src, ''))                             # 3.
while len(queue) > 0:                               # 4.0
    first, path = queue[0]
    if first == dest:                               # Handle reaching dest
        print(path)
    visited.add(first)                              # 4.1
    for index in range(len(call_graph[first])):     # Require index
        reachable = call_graph[first][index]
        if reachable not in visited:
            char = 'NEWS'[index]                    # To get NEWS[index] for path
            queue.append((reachable, path + char))  # 4.2
    del queue[0]

Finally, running this code gives

SSSSEENNEESSSSEENNEEEEEEEESSSSEESSSSWWSSSSEESSEESSSSWWSSSSWWWWWWSSWWSSSSSSEEEESSSSEESSEESSSSSSSSEENNEESSEEEESSEESSSSEESSEEEEEEEESSEEEESSSSEEEEEENNNNNNEENNWWNNEEEENNNNEEEENNEEEEEESSSSWWSSWWSSSSEEEESSWWSSEESSEEEESSSSEENNNNNNEEEESSEESSEESSEEEESSEENNEENNWWNNEEEEEESSEEEEEENNNNWWWWNNWWNNNNWWNNEEEEEENNEENNWWWWNNWWNNEENNEEEEEEEESSEESSEESSSSEESSEEEEEENNEESSSSSSEEEEEENNNNNNNNNNNNNNNNEEEEEEEEEEEESSEESSSSWWWWSSSSSSWWSSEESSEEEEEENNNNEESSEESSEEEENNEENNNNEEEEEENNEENNWWWWWWNNNNWWSSSSWWSSSSWWWWNNNNNNNNNNEENNEENNEENNEEEESSEESSSSEEEEEESSEEEEEEEENNNNEENNNNWWNNEEEENNNNEEEEEESSSSSSSSSSSSSSSSSSSSSSEESSSSEEEEEESSEESSWWSSSSEESSSSEEEENNEEEESSWWSSSSSSSSWWSSWWWWWWSSWWWWSSWWNNNNWWWWWWSSEESSWWSSWWSSEESSSSSSSSSSWWSSEEEESSSSSSEEEESSSSEESSEESSSSEEEESSEENNEEEESSSSWWSSEESSWWSSSSWWWWNNWWSSSSEESSEEEESSWWSSSSWWWWNNWWNNWWSSSSWWWWWWWWWWWWWWSSSSSSWWWWSSEESSWWSSWWWWWWSSWWWWWWWWSSSSEESSEEEEEESSSSSSEEEESSSSEEEEEESSWWWWSSSSSSSSSSSSEEEEEESSEEEENNEEEENNEEEENNEEEENNEEEESSEENNEEEESSSSSSSSWWSSWWSSSSWWSSSSSSEESSSSEEEESSEENNEESSEEEE

We can then submit to the remote server for the flag.

❯ python3 "python3 solve.py"
[+] Opening connection to chalp.hkcert21.pwnable.hk on port 28117: Done
hkcert21{4lw4ys_l0ok_4t_s74ck_0verf1ow_wh3n_y0u_w4nt_t0_4v01d_s7ack_0v3rfl0ws}
[*] Closed connection to chalp.hkcert21.pwnable.hk port 28117

Flag: hkcert21{4lw4ys_l0ok_4t_s74ck_0verf1ow_wh3n_y0u_w4nt_t0_4v01d_s7ack_0v3rfl0ws}

Remarks

If the graph is weighted, other algorithms would have to be used.

Thank you Mystiz for the challenge!