Modular Forms
I have decided to take on the topic of Modular Forms. I don’t intend to dive too in depth into the topic, since it is obviously a rich theory and has many prerequisites. However, I will try to get a basic understanding of what is it about and what the theory tries to answer.
References: Kilford (Book), Conrad (Notes), Conrad (Videos), Borcherds (Videos).
Prerequisites
We begin by considering the modular group \(\mathrm{SL}_2(\mathbb{Z})\), defined as all \(2 \times 2\) matrices with determinant \(1\):
\[ \mathrm{SL}_2(\mathbb{Z}) = \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} : a, b, c, d \in \mathbb{Z}, ad - bc = 1 \right\} \]
Here, \(\mathrm{SL}\) stands for the Special Linear Group. It is also common to denote the group by \(\Gamma\) and elements of \(\mathrm{SL}_2(\mathbb{Z})\) by \(\gamma\).
It is known that \(\mathrm{SL}_2(\mathbb{Z})\) is finitely generated by matrices \(T = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}\) and \(S = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\).
Next, we define the Poincaré upper half plane as \(\mathcal{H} = \{z \in \mathbb{C} : \Im(z) > 0\} \cup \{\infty\}\). We note that \(\mathrm{SL}_2(\mathbb{Z})\) acts on \(\mathcal{H}\) by
\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix}(z) = \frac{az + b}{cz + d}, \quad \text{for } z \in \mathbb{C} \]
And the extended definitions \(\gamma(-d / c) = \infty\) and \(\gamma(\infty) = a / c\). These are the Möbius transformations or linear fractional transformations. Of course, we have to verify that \(z \in \mathcal{H}\) implies \(\gamma(z) \in \mathcal{H}\). This follows from the identity
\[ \Im\left(\frac{az + b}{cz + d}\right) = \Im\left(\frac{(ac)\|z\|^2 + (ad)z + (bc)\overline{z} + bd}{\|cz + d\|^2}\right) = \frac{(ad - bc)\Im(z)}{\|cz + d\|^2} > 0 \]
Basic Definitions
Next, we present the important definitions.
Definition: If \(f : \mathcal{H} \to \mathbb{C}\) is a meromorphic holomorphic in all but a discrete finite subset function which satisfies the transformation formula
\[ f\left(\frac{az + b}{cz + d}\right) = (cz + d)^k f(z), \quad \text{for } \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \mathrm{SL}_2(\mathbb{Z}), z \in \mathcal{H} \]
Thne we say that \(f\) is weakly modular of weight \(k\) (for \(\mathrm{SL}_2(\mathbb{Z})\). In particular, by considering the matrices \(T, S\) and \(S^2\), we obtain the following equations:
\begin{align} f(z + 1) &= f(z) \\ af\left(-\frac{1}{z}\right) &= (-z)^k f(z) \\ f(z) &= (-1)^k f(z) \end{align}
In particular, by (3) we know that there are no weakly modular forms of odd weight. It can also be shown that if \(f\) satisfies \(1\) and \(2\), then it is weakly modular for \(\mathrm{SL}_2(\mathbb{Z})\), following from that \(S\) and \(T\) generate \(\mathrm{SL}_2(\mathbb{Z})\).
Definition: We say that a meromorphic function \(f: \mathcal{H} \to \mathbb{C}\) is a modular form of weight \(k\) (for \(\mathrm{SL}_2(\mathbb{Z})\)) if it satisfies the following:
-
\(f\) is weakly modular of weight \(k\) for \(\mathrm{SL}_2(\mathbb{Z})\).
-
\(f\) is holomorphic on \(\mathcal{H}\).
-
The values \(f(\gamma)\) are bounded as \(\Im(\gamma) \to \infty\).
We denote the set of modular form sof weight \(k\) for \(\mathrm{SL}_2(\mathbb{Z})\) by \(M_k(\mathrm{SL}_2(\mathbb{Z}))\).
Furthermore, we define the value of \(f(z)\) at \(\infty\) to be \(f(\infty) := \lim_{z \to i\infty} f(z)\). If \(f(\infty) = 0\), then we say that \(f\) is a cusp form of weight \(k\) (for \(\mathrm{SL}_2(\mathbb{Z})\)). The set of cusp forms is written as \(S_k(\mathrm{SL}_2(\mathbb{Z}))\).
The third condition above, also called the modularity condition, can be written as \(\gamma \to i\infty\), or that \(f\) is holomorphic at \(i\infty\). Now, since \(f\) is periodic with period \(1\), it has a Fourier series
\[ f(q) = \sum_{n \geq 0} a_n q^n, \quad \text{with } q := \exp(2\pi iz) \]
(There is an abuse of notation denoting both \(f(z)\) and \(f(q)\) with \(f\).) This is called the \(q\)-expansion of \(f\), and the coefficients \(a_n\) are called the Fourier coefficients of \(f\). Moreover, one can prove that the sum converges for every \(z \in \mathcal{H}\) - see Conrad, 4.5 & 4.6.
[ERROR] 唉屌又error
Clarify the proof of \(q\)-expansion from Conrad’s notes.
Normally, such a Fourier series is indexed by \(n \in \mathbb{Z}\). However, since \(f\) is holomorphic at \(i\infty\), for every negative \(n\) we have \(a_n = 0\). Also, note that \(a_0 = f(q = 0) = f(z = i\infty)\). As such, if \(a_0 = 0\), we say that \(f\) vanishes at \(\infty\), which also means that \(f\) is a cusp form.
Eisenstein Series
It is useless to write down random definitions without usage. Therefore, it is natural to ask whether modular forms actually exist. By definition, we see that all constant functions are modular forms of weight \(0\), meaning \(M_0(\mathrm{SL}_2(\mathbb{Z})) \supseteq \mathbb{C}\). We will later see that this is an inequality. However, now we should focus on finding modular forms of nonzero weights.
Definition: For even \(k \geq 4\), we define the weight \(k\) Eisenstein series as
\[ G_k(z) := \sum_{(m, n) \in \mathbb{Z}^2 \setminus \{(0, 0)\}} (mz + n)^{-k} \]
We shall show that this is a nonzero modular form of weight \(k\) for \(\mathrm{SL}_2(\mathbb{Z})\). The proof boils down to checking each of the three conditions in the definition is satisfied.
Actually, before we do that, let’s look at our definition. Firstly, why do we require \(k \geq 4\)? As we will see later, this is because for \(k = 2\), the sum does not converge absolutely, which means the sum is not well defined. Why do we require \(k\) to be even then? Well, the definition makes sense for \(k \geq 3\), but when \(k\) is odd, the terms for \((m, n)\) and \((-m, -n)\) cancel out, meaning the series vanishes and \(G_k(z) = 0\). This matches our observation above that there are no modular forms of odd weight.
Proposition: Let \(\Lambda \subseteq \mathbb{Z}^n\) be a lattice. The series
\[ L := \sum_{0 \neq \rho \in \Lambda} \|\rho\|^{-t} \]
is absolutely convergent for \(t > k\).
[SUCCESS] 搞掂!
Proof 1: We follow Serre, Chapter VII with assistance from jschnei and hellman. We first prove that for integer \(n\), the number of elements of \(\Lambda\) such that \(k \leq \|\rho\| < k + 1\) is \(\mathcal{O}_{\Lambda}(k^{n - 1})\). To do this, we first define \(d := \min\{\|z_1 - z_2\| : z_1 \neq z_2 \in \Lambda\}\). We then draw a hypersphere of radius \(d / 2\), denoted \(\mathcal{B}_z(d / 2)\), around each point \(z\) of the lattice. By definition, the hyperspheres don’t overlap. Next, we define the belt \(\mathcal{C} := \{z : k \leq \|z\| < k + 1\} = \mathcal{B}_{k + 1} \setminus \mathcal{B}_k\). We note that the hypervolume of \(\mathcal{C}\) is
\[ \mathrm{Vol}(\mathcal{C}) = \frac{\pi^{n / 2}}{\Gamma\left(\frac{n}{2} + 1\right)} \left((k + 1)^n - k^n\right) = \mathcal{O}_{\Lambda}(k^{n - 1}) \]
To finish off the proof, note that there are at most \(\mathrm{Vol}(\mathcal{C}) / \min\{|\mathcal{C} \cap \mathcal{B}_z(d / 2)| : z \in \Lambda\}\) lattice points in \(\mathcal{C}\), which is again \(\mathcal{O}_{\Lambda}(k^{n - 1})\). This means that there is a constant \(C_{\Lambda}\) such that the number of lattice pints in \(\mathcal{C}\) is at most \(C_{\Lambda}k^{n - 1}\). We can now obtain the upper bound
\[ L < \sum_{k \geq 0} \frac{C_{\Lambda}k^{n - 1}}{k^t} = C_{\Lambda} \sum_{k \geq 0} k^{n - 1 - t} \]
which converges for \(t > k\).
[SUCCESS] 搞掂!
Proof 2: We follow C-RAM’s answer. Write \(\Lambda = \mathbb{Z}\vec{v_1} + \cdots + \mathbb{Z}\vec{v_n}\) and \(\vec{\mathbf{x}} = (x_1, \cdots, x_n)\). We note that \(\|\cdot\|_{\Lambda} : \vec{\mathbf{x}} \mapsto \left\|\sum_{i = 1}^n x_i\vec{v_i}\right\|\) is a norm on \(\mathbb{R}^n\). Now, since any two norms on \(\mathbb{R}^n\) are equivalent, there exists a constant \(M\) such that \(M\|(x, y)\|_{\Lambda} \geq \max \vec{\mathbf{x}}\). Therefore,
\begin{align*} L &= \sum_{\vec{\mathbf{x}} \in \mathbb{Z}^n \setminus \{0\}} \frac{1}{\|\vec{\mathbf{x}}\|_{\Lambda}^t} \\ &\leq \frac{1}{M^t} \sum_{1}{M^t} \sum_{\vec{\mathbf{x}} \in \mathbb{Z}^n \setminus \{0\}} \frac{1}{(\max \vec{\mathbf{x}})^t} \\ &= \frac{1}{M^t} \sum_{k = 1}^{\infty} \frac{(2k + 1)^n - (2k - 1)^n}{k^t} \\ &= \frac{1}{M^t} \sum_{k = 1}^{\infty} \frac{n 2^n k^{n - 1} + \mathcal{O}(k^{n - 3})}{k^t} \end{align*}
Which again converges for \(t > k\).
Back to the task of proving that \(G_k(z)\) is a nonzero modular form of weight \(k\) for \(\mathrm{SL}_2(\mathbb{Z})\). We are now ready to prove that it is holomorphic!
Suppose that \(z \in \mathbb{C}\) satisfies \(\|z\| \geq 1\) and \(|\Re(z)| \leq \frac{1}{2}\), as shaded blue below. This region \(F\) is a fundamental domain of \(\mathrm{SL}_2(\mathbb{Z})\), which we will rigorously define later. For now, we see that for \(z \in F\), we have
\[ \|mz + n\|^2 = m^2 z\overline{z} + 2mn\Re(z) + n^2 \geq m^2 - mn + n^2 = \|m\omega - w\|^2 \]
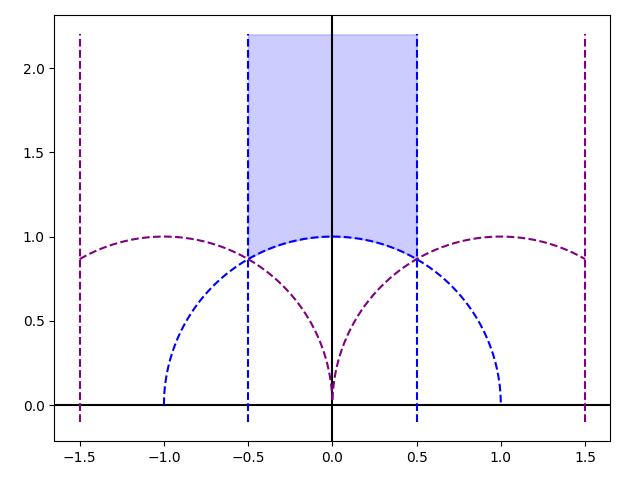
Next, we show that \(G_k(z)\) is holomorphic at \(i\infty\). Consider the series definition when \(z \to i\infty\). When \(m \neq 0\), the term \((mz + n)^{-k}\) contributes \(0\) to the sum, while when \(m = 0\), it contributes \(n^{-k}\). Therefore, we have \(\lim_{z \to i\infty} G_k(z) = 2\zeta(k)\). Neat!
Finally, we show that \(G_k(z)\) is weakly modular for \(\mathrm{SL}_2(\mathbb{Z})\), which requires showing that \(G_k(z + 1) = G_k(z)\) and \(G_k\left(-\frac{1}{z}\right) = z^k G_k(z)\). Here, \(G_k(z)\) being absolutely convergent allows us to rearrange the terms. For the first condition, note that
\begin{align*} G_k(z + 1) &= \sum_{(m, n) \neq (0, 0)} \left(m(z + 1) + n\right)^{-k} \\ &= \sum_{(m, n) \neq (0, 0)} \left(mz + (m + n)\right)^{-k} \\ &= \sum_{(m, n’) \neq (0, 0)} \left(mz + n’\right)^{-k} \\ &= G_k(z) \end{align*}
For the second condition, we expand
\begin{align*} G_k\left(-\frac{1}{z}\right) &= \sum_{(m, n) \neq (0, 0)} \left(-\frac{m}{z} + n\right)^{-k} \\ &= \sum_{(m, n) \neq (0, 0)} z^k(-m + nz)^{-k} \\ &= z^k \sum_{(m’, n) \neq (0, 0)} (nz + m’)^{-k} \\ &= z^k G_k(z) \end{align*}
[INFO] 李家超提提你
Starting from here, one can expand to get the \(q\)-expansion of \(G_k(z)\). Also, by observing the first few coefficients of the first few Eisenstein series, one can deduce and prove that the set of modular forms actually form a graded ring. Finally, there is a simple characterisation of the dimension of \(M_n(\mathrm{SL}_2(\mathbb{Z}))\), which can be proven by applying the Residue theorem.