Shares V1 (216 pts, 29 solves) / V2 (804 pts, 15 solves)

January 02, 2022

Introduction

Our team Black Bauhinia participated in the TetCTF 2022 which spans two days. Shares is an interesting two-part challenge. Mystiz and I (grhkm) spent around 10 hours in total on this challenge, $4$ on the first part and $6$ on the second.

Problem Statements

Description: Yet another secret sharing scheme.

Service: nc 139.162.61.222 13371

Binary: https://drive.google.com/file/d/1sP0zKSKoF6TJZ-gtaUf7rv4dQ-bGr-cp/view?usp=sharing

Description: A new feature is added. Check it out!

Service: nc 139.162.61.222 13372

Binary: https://drive.google.com/file/d/1FfHxyt3mWFGzxK6DwkZ3wZ77IICYjaJA/view?usp=sharing

V1 - Solution Outline

There is a high probability that there are more than $16$ singular matrices out of $2022$ matrices over $\mathbb{F}_{37}$. We are then able to eliminate the random variables and obtain more than $16$ equations on the password, which is then solved easily.

Problem Objective

We are given a single script shares.py. I have prettified the code below:

from random import randint

p = 37
ALLOWED_CHARS = "abcdefghijklmnopqrstuvwxyz0123456789_"
INT_TO_CHAR = {}
CHAR_TO_INT = {}
for _i, _c in enumerate(ALLOWED_CHARS):
    INT_TO_CHAR[_i] = _c
    CHAR_TO_INT[_c] = _i

def get_shares(pwd):
    ffes = [CHAR_TO_INT[c] for c in pwd]
    ffes += [randint(0, 36) for _ in range(32 - len(pwd))]
    result = []
    for _ in range(16):
        coeffs = [randint(0, 36) for _ in range(len(ffes))]
        s = sum([x * y for x, y in zip(coeffs, ffes)]) % P
        coeffs.append(s)
        result.append("".join(INT_TO_CHAR[i] for i in coeffs))
    return result

pwd = "".join(INT_TO_CHAR[randint(0, 36)] for _ in range(16))
for _ in range(2022):
    line = input()
    if line == pwd:
        FLAG = 'FLAG' * 30
        print(FLAG)
        return
    else:
        print(get_shares(pwd))

From here onwards, char stands for one of the $37$ allowed characters, while int stands for an integer between $0$ and $36$.

As we see in the source, a $16$-char password $c_1c_2\ldots c_{16}$ is fixed at the start and our goal is to guess it. We can also obtain $2021$ shares get_shares(pwd), where:

Appends $16$ random chars to the password
- $P = c_1c_2\ldots c_{16}r_1r_2\ldots r_{16}$
Generates $16$ random 32-int vectors $v_1, v_2, \ldots, v_{16}\in(\mathbb{Z} / 37\mathbb{Z})^{32}$
returns $\{v_1, v_2, \ldots, v_{16}\}$ as well as $\{s_i\}_i = \{v_i\cdot P\}_i$.

Variable	Known?
$c_i \in [0, 36]$	Unknown, our goal
$r_i \in [0, 36]$	Unknown
$v_i = \{v_{i, 1}, v_{i, 2}, \ldots, v_{i, 16}\}$	Known
$s_i = \sum_{1\leq j\leq 16} v_{ij}P_j$	Known

$\begin{pmatrix} A & lot & of & equations \end{pmatrix}$

Consider a single share of get_shares(pwd). Notice that although we have $16$ equations and $32$ unknowns, $16$ of the unknowns are just the password, which we will treat as constants for now. (It will be apparent why soon). However, even after this improvement we still have $16$ equations and $16$ unknowns, just short of what’s needed to eliminate the random chars.

$$\begin{cases}v_{1, 17}r_1 + v_{1, 18}r_2 + \cdots + v_{1, 32}r_{16} &= s_1 - \big(v_{1, 1}c_1 + v_{1, 2}c_2 + \cdots + v_{1, 16}c_{16}\big) \\ v_{2, 17}r_1 + v_{2, 18}r_2 + \cdots + v_{2, 32}r_{16} &= s_2 - \big(v_{1, 1}c_1 + v_{2, 2}c_2 + \cdots + v_{2, 16}c_{16}\big) \\ \cdots &= \cdots \\ v_{16, 17}r_1 + v_{16, 18}r_2 + \cdots + v_{16, 32}r_{16} &= s_{16} - \big(v_{16, 1}c_1 + v_{16, 2}c_2 + \cdots + v_{16, 16}c_{16}\big)\end{cases}$$

As always, let’s write it in matrix form and see what insights we get:

$$\begin{pmatrix} v_{1, 17} & v_{1, 18} & \cdots & v_{1, 32} \\ v_{2, 17} & v_{2, 18} & \cdots & v_{2, 32} \\ \vdots & \vdots & \ddots & \vdots \\ v_{16, 17} & v_{16, 18} & \cdots & v_{16, 32} \end{pmatrix}\begin{pmatrix} r_1 \\ r_2 \\ \vdots \\ r_{16}\end{pmatrix} = \begin{pmatrix}s_1 - \big(v_{1, 1}c_1 + v_{1, 2}c_2 + \cdots + v_{1, 16}c_{16}\big) \\ s_1 - \big(v_{2, 1}c_1 + v_{2, 2}c_2 + \cdots + v_{2, 16}c_{16}\big) \\ \vdots \\ s_1 - \big(v_{16, 1}c_1 + v_{16, 2}c_2 + \cdots + v_{16, 16}c_{16}\big)\end{pmatrix}$$

Well, since every $r_i$ and $c_j$ are unknown, there is no way we can do anything! The random chars are unknown and the right-hand side is unknown…

Discord Spam ft. Random Ideas (that worked?)

I realized the trick… ft. Duality of grhkm

WAIT! Consider the $v_{i, j}$ matrix in Row Echelon Form (i.e. after Gaussian Elimination). If the matrix does not have full-rank, there must be a zero row $(0, 0, \ldots, 0)$, which when multiplied by (the transformed) $\vec{r}$ must also give $0$.

For clarity, I will provide an example. Consider the system of equations

$$\begin{cases} x + y + z &= 3 + t \\ 2x + y + z &= 5 - 2t \\ 3x + y + z &= 4 + t\end{cases},$$

where $t$ is a variable like the right-hand side vector above. Transforming this into a Reduced Echelon Form:

$$\begin{cases} x + y + z &= 3 + t \\ y + z &= 1 + 4t \\ 2y + 2z &= 5 + 2t\end{cases}$$

$$\begin{cases} x + y + z &= 3 + t \\ y + z &= 1 + 4t \\ 0 &= 3 - 6t\end{cases}$$

As we can see, since the original matrix $\begin{pmatrix}1 & 1 & 1 \\ 2 & 1 & 1 \\ 3 & 1 & 1\end{pmatrix}$ is singular, we have a zero-row at the end, giving us $3 - 6t = 0$, which is useful!!

But what’s the chance of this happening? Well, we know that $k$ linearly independent vectors span a space of $p^k$ vectors, so by a simple exclusion we have that

$$P(\det V = 0) = 1 - \prod_{k=0}^n (1 - p^{k - n}) = 0.02775\ldots\approx\frac{1}{36}$$

So on average, we can expect $56$ singular matrices, giving us a lot of equations in $c_1, c_2, \cdots, c_{16}$! Afterwards, it is easy to solve for $c_i$, recover the password, submit and get the flag.

Code

from pwn import *
from tqdm import tqdm

# local runs in 30 seconds, remote takes 20 minutes
r = remote('139.162.61.222', 13371)
# r = process('pypy3 shares.py', shell=True)

P = 37
CHARS = "abcdefghijklmnopqrstuvwxyz0123456789_1"
def INT_TO_CHAR(i): return CHARS[i]
def CHAR_TO_INT(c): return CHARS.index(c)


lhs, rhs = [], []
tq = tqdm(range(2000))
cnt = 0
for _ in tq:
    r.sendline(b'a')
    rv = eval(r.recvline())
    # Notice I keep the c1, c2, ..., c16 coefficients as vectors
    rv = [[CHAR_TO_INT(c) for c in r] for r in rv]
    cs = Matrix(GF(P), [r[16:32] for r in rv])
    # Singular?
    if cs.rank() < 16:
        rs = Matrix(GF(P), [r[:16] + [r[-1]] for r in rv])
        res = cs.augment(rs).rref()[-1]
        # first 16 columns are the v_{i, j}
        lhs.append(res[16:32])
        rhs.append(res[32])
        if len(lhs) == 16:
            break
    cnt += 1
    tq.set_description(f"{len(lhs)} / {cnt}")

# solve for password
ref = Matrix(GF(P), lhs).solve_right(vector(GF(P), rhs))
pwd = ''.join((INT_TO_CHAR(r) for r in ref))
r.sendline(pwd.encode())
print("Flag:", r.recvline().decode())

Flag: TetCTF{m0r3_sh4r3s____m0r3_m0r3_m0r3_fun}

V2 - Solution Outline

We split the coefficients’ matrix into two halves and perform a Meet In The Middle (MITM) attack.

Problem Objective

We are given an updated script shares_v2.py. Here is the cleaned up code:

def get_shares_v2(pwd):
    ffes = [CHAR_TO_INT(c) for c in pwd]
    result = []
    for _ in range(32):
        coeffs = [randint(0, 36) for _ in range(len(ffes))]
        s = sum([x * y for x, y in zip(coeffs, ffes)]) % 37
        coeffs.append(s)
        result.append("".join(INT_TO_CHAR(i) for i in coeffs))
    
    master = randint(0, (1 << 128) - 1)
    shares = []
    for i, share in enumerate(result):
        v = CHAR_TO_INT(share[-1])
        if (master >> i) & 1:
            v = (v + 18) % 37
        shares.append(share[:-1] + INT_TO_CHAR(v))
    return shares

pwd = "".join(INT_TO_CHAR(randint(0, 36)) for _ in range(32))
for _ in range(2022):
    line = input()
    if line == pwd:
        FLAG = 'FLAG' * 30
        print(FLAG)
    else:
        print(get_shares_v2(pwd))

The structure of the code is similar to v1. However, there are three key differences:

The random bits have been removed and password is now 32-char
- $P = c_1c_2\ldots c_{32}$
$32$ dot products are given instead of $16$. However,
Each dot product $s_i$ has a chance of having $18$ added to it
- In other words, random bits $r_1, r_2, \ldots, r_{32} \in \{0, 1\}$ are chosen, and each $s_i \mapsto s_i + 18r_i$

Variable	Known?
$c_i \in [0, 36]$	Unknown, our goal
$v_i = \{v_{i, 1}, v_{i, 2}, \ldots, v_{i, 16}\}$	Known
$r_i \in \{0, 1\}$	Unknown
$s_i = 18r_i + \sum_{1\leq j\leq 16} v_{ij}P_j$	Known

Writing the $32$ relations together as matrices and vectors, we have

$$\vec{s} = 18\vec{r} + VP^T.$$

The first thing that comes to mind is to bruteforce all possible $\vec{r}$, since there are only $2^{32}$ possibilities. We can then compute $P^T = V^{-1}(\vec{s} - 18\vec{r})$. However, how do we know if such password is correct? Well, notice that if we are given two shares:

$$\begin{cases}\vec{s_1} = 18\vec{r_1} + V_1P^T \\ \vec{s_2} = 18\vec{r_2} + V_2P^T \end{cases}$$

We can then substitute a particular guess into the second share to get

$$\vec{s_2} = 18\vec{r_2} + V_2V_1^{-1}(\vec{s_1} - 18\vec{r_1})$$

$$\fbox{$18\vec{r_2} = \vec{s_2} - V_2V_1^{-1}(\vec{s_1} - 18\vec{r_1})$}$$

Where every component on the right-hand side is known (and $\vec{r_1}$ is our guess). We can then simply check if each entry in the vector is either $0$ or $18$.

However, this is too slow! A rough estimate of the operations show that brute forcing has a time complexity of $O(2^n\cdot n^3)\approx 1.4\cdot 10^{14}$. Since we wasted all our money last year on other CTFs, we are unable to rent expensive $100$-core machines, and $1.4\text{e}14$ operations will definitely take too long.

Mystiz Is The Best 😘

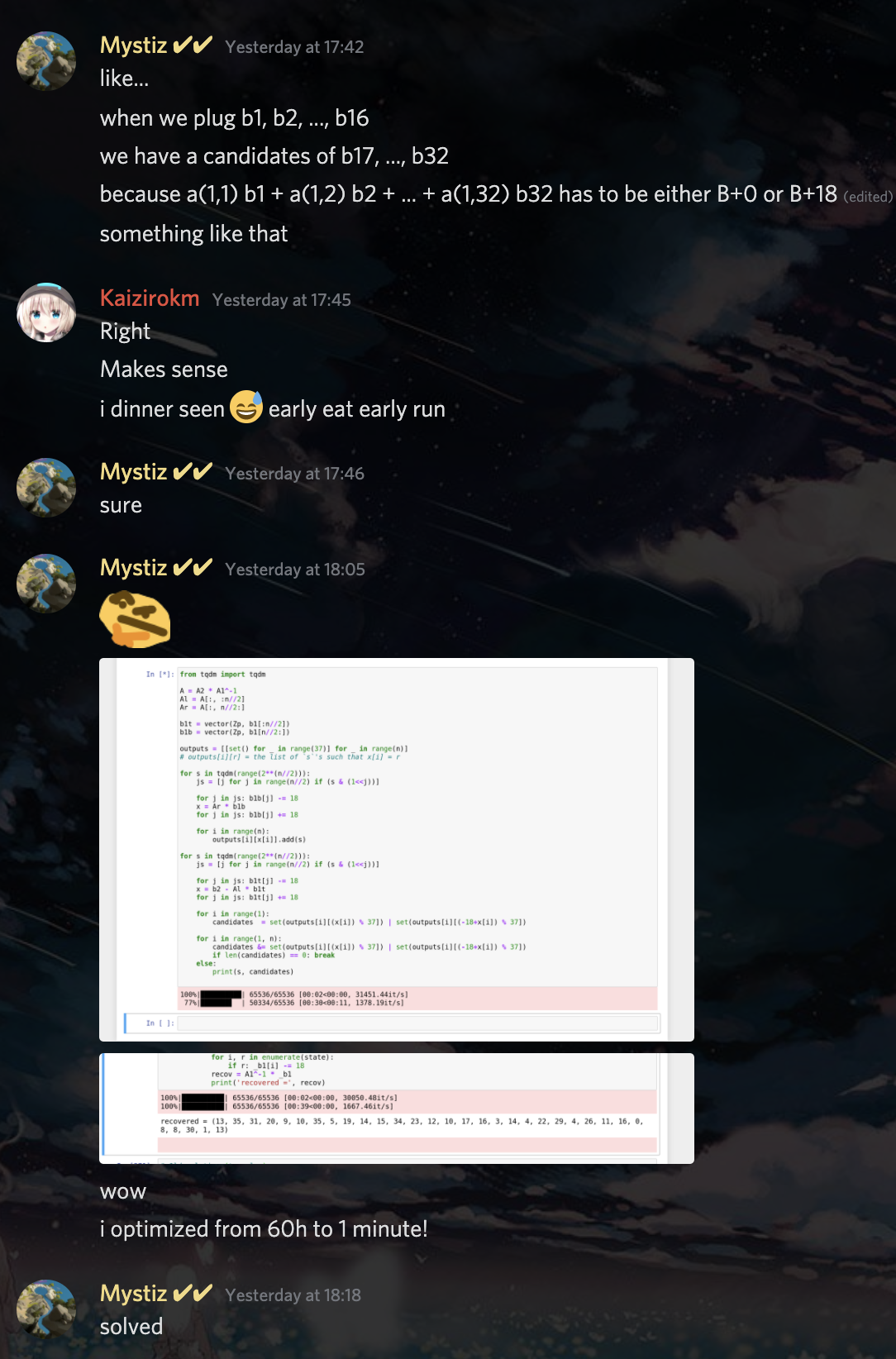
However, here comes Mystiz to the rescue!

It is clear that we have to do some kind of Meet In the Middle (MITM) attack. However, it is not immediately clear how to divide into sub-problems. Let’s take a look at matrix multiplication for inspirations:

$$\begin{align*} &\begin{pmatrix}v_{1, 1} & v_{1, 2} & \cdots & v_{1, 2n} \\ v_{2, 1} & v_{2, 2} & \cdots & v_{2, 2n} \\ \vdots & \vdots & \ddots & \vdots \\ v_{2n, 1} & v_{2n, 2} & \cdots & v_{2n, 2n}\end{pmatrix}\begin{pmatrix}r_1 \\ r_2 \\ \vdots \\ r_{2n}\end{pmatrix} \\ &= \begin{pmatrix}r_1v_{1, 1} + r_2v_{1, 2} + \cdots + r_{2n}v_{1, 2n} \\ r_2v_{2, 1} + r_2v_{2, 2} + \cdots + r_{2n}v_{2, 2n} \\ \vdots \\ r_1v_{2n, 1} + r_2v_{2n, 2} + \cdots + r_{2n}v_{2n, 2n}\end{pmatrix} \\ &= \begin{pmatrix}(r_1v_{1, 1} + \cdots + r_{n}v_{1, n}) + (r_{n + 1}v_{1, n + 1} + \cdots + r_{2n}v_{1, n}) \\ (r_1v_{2, 1} + \cdots + r_{n}v_{2, n}) + (r_{n + 1}v_{2, n + 1} + \cdots + r_{2n}v_{2, 2n}) \\ \vdots \\ (r_1v_{2n, 1} + \cdots + r_{n}v_{2n, n}) + (r_{n + 1}v_{2n, n + 1} + \cdots + r_{2n}v_{n, n})\end{pmatrix} \\ &= \begin{pmatrix}v_{1, 1} & v_{1, 2} & \cdots & v_{1, n} \\ v_{2, 1} & v_{2, 2} & \cdots & v_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ v_{2n, 1} & v_{2n, 2} & \cdots & v_{2n, n}\end{pmatrix}\begin{pmatrix}r_1 \\ r_2 \\ \vdots \\ r_n\end{pmatrix} + \begin{pmatrix}v_{1, n + 1} & v_{1, n + 2} & \cdots & v_{1, 2n} \\ v_{2, n + 1} & v_{2, n + 2} & \cdots & v_{2, 2n} \\ \vdots & \vdots & \ddots & \vdots \\ v_{2n, n + 1} & v_{2n, n + 2} & \cdots & v_{2n, 2n}\end{pmatrix}\begin{pmatrix}r_{n + 1} \\ r_{n + 2} \\ \vdots \\ r_{2n}\end{pmatrix}\end{align*}$$

That’s an unnecessarily convoluted mess! Simply put, we have

$$[M_L | M_R]\left(\frac{v_L}{v_R}\right) = M_Lv_L + M_Rv_R$$

Where each term on the right-hand side is half the size of the original matrix and vector. Looking back at our equation:

$$\vec{s_2} - V_2V_1^{-1}(\vec{s_1} - 18\vec{r_1}) = 18\vec{r_2}$$

Let’s denote $M := V_2V_1^{-1}$. Then using the same notation as above, we have:

$$M_L(\vec{s_{1L}} - 18\vec{r_{1L}}) + M_R(\vec{s_{1R}} - 18\vec{r_{1R}}) = \vec{s_2} - 18\vec{r_2}.$$

Now the strategy is clear:

Iterate through all $r_{1L}$
Store the $\vec{v} = M_L(\vec{s_{1L} - 18\vec{r_{1L}}})$ into a data structure.
For each $\vec{r_{1R}}$,
- Test if there is a $\vec{v}$ such that $M_R(\vec{s_{1R}} - 18\vec{r_{1R}}) = \vec{s_2} - \vec{v} - [0 / 18]$ by testing each row sequentially.
- If such vector is found, simply combine to get $\vec{r_1}$ and recover $P^T = V_1^{-1}(\vec{s_1} - 18\vec{r_1})$.

Code

import itertools
from pwn import *
from tqdm import tqdm

p = 37
CHARS = "abcdefghijklmnopqrstuvwxyz0123456789_"
def INT_TO_CHAR(i): return CHARS[i]
def CHAR_TO_INT(c): return GF(p)(CHARS.index(c))

r = remote('139.162.61.222', 13372)
# r = process('pypy3 shares-v2.py', shell=True)

# parse data
r.sendline(b'a\na')
V1, V2, s1, s2 = [], [], [], []
for row1, row2 in zip(eval(r.readline()), eval(r.readline())):
    row1 = list(map(CHAR_TO_INT, row1))
    row2 = list(map(CHAR_TO_INT, row2))
    V1.append(row1[:32])
    V2.append(row2[:32])
    s1.append(row1[32])
    s2.append(row2[32])

V1, V2 = Matrix(V1), Matrix(V2)
s1, s2 = vector(s1), vector(s2)

assert V1.determinant() != 0 and V2.determinant() != 0
M = V2 * V1 ** -1
sl, sr = s1[:16], s1[16:]
Ml, Mr = M[:, :16], M[:, 16:]
# cand[row][k] stores candidates of r where (s1l - 18 * r)[row] = k
cand = [[set() for _ in range(37)] for _ in range(32)]

tq = tqdm(itertools.product(*[[Mod(0, p), Mod(1, p)] for k in range(16)]), total=int(1 << 16))
for r1l in tq:
    # prevent timeout
    if tq.n % (1 << 12) == 0:
        r.sendline(b'a')
        r.recvline()
    # storing candidates into correct slot
    v = Ml * (sl - 18 * vector(r1l))
    for i in range(32):
        cand[i][v[i]].add(r1l)

# precompute for queries pre[row][k] -> (s1l - 18 * r)[row] = k OR k - 18
pre = [[cand[i][j] | cand[i][(j - 18) % 37] for j in range(37)] for i in range(32)]

tq = tqdm(itertools.product(*[[Mod(0, p), Mod(1, p)] for k in range(16)]), total=int(1 << 16))
for r1r in tq:
    # prevent timeout
    if tq.n % (1 << 12) == 0:
        r.sendline(b'a')
        r.recvline()
    # testing if v exists
    res = s2 - Mr * (sr - 18 * vector(r1r))
    cand = set()
    # testing rows sequentially
    for i in range(32):
        st = pre[i][res[i]]
        if i == 0:
            cand |= st
        else:
            cand &= st
        if len(cand) == 0:
            break
    else:
        # recover password
        r1l = list(cand)[0]
        r1 = vector(GF(p), list(r1l) + list(r1r))
        rvec = V1 ** -1 * vector(GF(p), s1 - 18 * r1)
        rstr = ''.join(map(INT_TO_CHAR, rvec)).encode()
        print(f"Sending password = {rstr}")
        r.sendline(rstr)
        # hopefully no timeout?
        res = r.recvline()
        r.close()
        print("Flag:", res.decode().strip())
        break

Flag: TetCTF{but_th3_m4st3r_sh4re_1s_n0t_fun_4t_4ll}

Conclusion

Thank you to the organizers of TetCTF for providing such great challenges. I don’t understand why V2 has so few solves though…